方法一：暴力递归（超时）

思路： 枚举所有可能的解码方案。枚举方法如下： 第一步：首先对 $1,2, \ldots 26$ 一共 $26$ 个数字，可以构建一个编码的字符串集合 $legalstr$ 。 第二步：对于任意的字符串，依次选择 开始的 $1$ 个字符 或者 开始的 $2$ 个字符 进行解码。 如果这 $1$ 字符或者 $2$ 个字符在 $legalstr$ 中，则表示可以编码，对剩下的字符串执行同样的操作； 如果不合法，就不能生出递归树的枝叶。 当剩余字符串长度为 $0$ 的时候就说明完成了解码，给计数器加 $1$。假设字符串长为 $n$，递归树如下图所示：

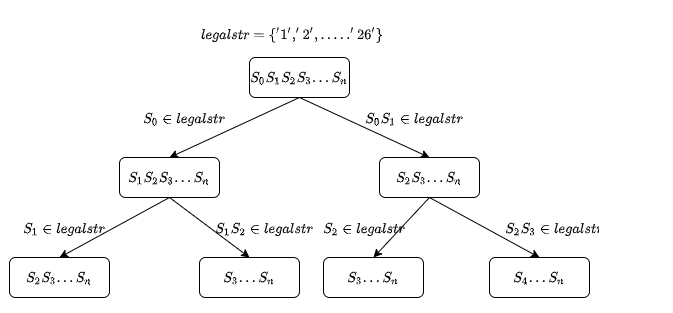
方法二：动态规划

思路与算法

对于给定的字符串 $s$，设它的长度为 $n$ ，其中的字符从左到右依次为 $s_1,s_2,\ldots s_n$。我们可以使用动态规划的方法计算出字符串 $s$ 的解码方法数。

具体地，设 $f_i$表示字符串 $s$ 的前 $i$ 个字符 $s_1 \ldots s_i$ 的解码方法数。在进行状态转移时，我们可以考虑最后一次解码使用了 $s$ 中的哪些字符，那么会有下面的两种情况：第一种情况是我们使用了一个字符，即 $s_i$ 进行解码，那么只要 $s_i \neq 0$，它就可以被解码成 $A∼I$ 中的某个字母。由于剩余的前 $i−1$ 个字符的解码方法数为 $f_{i−1}$ , 因此我们可以写出状态转移方程： $f_i = f_{i−1}$ 其中 $s_i \neq 0$

第二种情况是我们使用了两个字符，即 $s_{i−1}$ 和 $s_i$ 进行编码。与第一种情况类似，$s_{i−1}$ 不能等于 0，并且 $s_{i−1}$ 和 $s_{i}$ 组成的整数必须小于等于 26，这样它们就可以被解码成 $J∼Z$ 中的某个字母。由于剩余的前 $i−2$ 个字符的解码方法数为 $f_{i−2}$ ，因此我们可以写出状态转移方程：

$f_i = f_{i−2}$ ,其中 $s_{i−1} \neq 0$ 并且 $10⋅s_{i−1}+s_{i}\le 26$

需要注意的是，只有当 $i>1$ 时才能进行转移，否则 $s_{i−1}$ 不存在。

将上面的两种状态转移方程在对应的条件满足时进行累加，即可得到 $f_i$ 的值。在动态规划完成后，最终的答案即为 $f_n$。细节:动态规划的边界条件为：$f_0$ 即空字符串可以有 $1$ 种解码方法，解码出一个空字符串。 同时，由于在大部分语言中，字符串的下标是从 $0$ 而不是 $1$ 开始的，因此在代码的编写过程中，我们需要将所有字符串的下标减去 $1$，与使用的语言保持一致。

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int mod = 998244353;
signed main()
{
	string s;
	cin>>s;
	int n = s.size();
	vector<int>f(n+1);
	f[0] = 1;
	for(int i = 1 ; i <= n ; i++ )
	{
		if(s[i-1] != 0)
		{
			f[i] += f[i-1];
			f[i]%=mod;
		}
		if(i>1 && s[i-2] != '0' && ((s[i - 2] - '0') * 10 + (s[i - 1] - '0') <= 26))
		{
			f[i] += f[i-2];
			f[i]%=mod;
		}
	}
	cout<<f[n]<<endl;
 }