DP捏

显然 到达任意的位置

只有从左边和从上面掉下来两条路子

不会真的有人傻到向左走吧

由于彩虹猫没法腾空

so 只有天花板和地板两条道路

（温馨提示：那个图就是个坑

你要真看这个图，那大约你也看不到下面的 了

读题是这道题最难的部分我说的

真的很难绷 上下蹿需要的是高度差大小的能量

向右跑不需要能量

网格图的意思是：

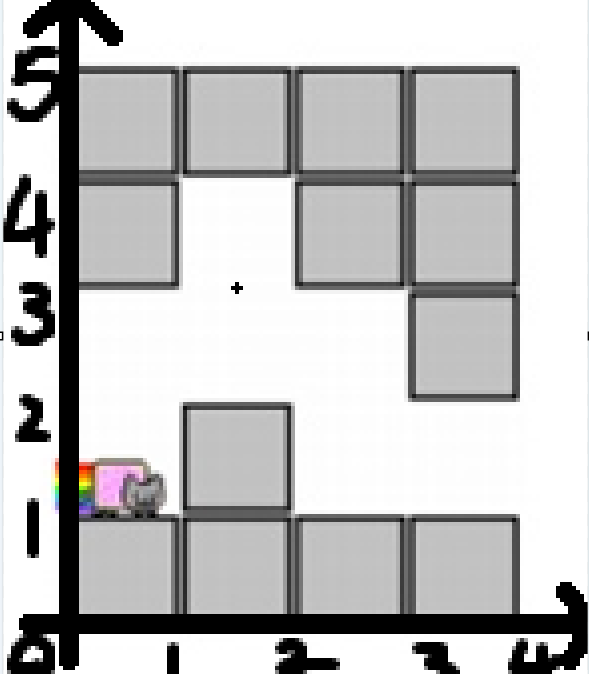
横坐标或许不用管，但是纵坐标挺坑的 注意：它看的是网格线，不是方格子

好的，知道了这些就足够码出一个dp了，只有两层还是线性的dp还要教吗？

Code

#include <iostream>
using namespace std;
const long long INF=1e17;
long long n,t[100114],f[100114];
long long dp[100114][3];
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>t[i];
		dp[i][1]=INF;
	}
	for(int i=1;i<=n;i++)
	{
		cin>>f[i];
		dp[i][2]=INF;
	}
	dp[1][1]=0;
	dp[1][2]=t[1]-f[1];
	for(int i=2;i<=n;i++)
	{
		if(f[i]<=f[i-1])
			dp[i][1]=dp[i-1][1];
		if(t[i]>=t[i-1])
			dp[i][2]=dp[i-1][2];
		dp[i][1]=min(dp[i][1],dp[i][2]+t[i]-f[i]);
		dp[i][2]=min(dp[i][2],dp[i][1]+t[i]-f[i]);
		if(t[i-1]<=f[i] || f[i-1]>=t[i])
			dp[i][1]=dp[i][2]=INF;//请注意这里的特判，会有彩虹猫被卡死的可能哦
	}
	if(dp[n][1]==INF)
		cout<<"-1";
	else
		cout<<dp[n][1];
	return 0;
}

解法一：

从起点开始dfs，每次选择向左右走或者反转重力，注意保证一条走法中同一个位置只经过一次这一剪枝，即可得到40~50分。

注意判断** 右侧下边界高于左侧上边界 和 右侧上边界低于左侧下边界 **这种不能通行的情况。

解法二：

可以将每个能走到的位置视为一个点，那么可行走的路线可以用单向边表示，左右走边权为0，反转重力边权为上下边界高度之差，用O(n^2)的最短路径算法即可得到60分。

解法三：

在解法二中用优化的最短路径算法即可得到100分。

解法四：

容易想到，在最优解法中，向左走是不会用到的，那现在只需要考虑反转重力或者向右走。

这是一个简单的线性dp，设f[i][0],f[i][1]分别为到达横坐标i的下、上边界需要的最小代价，因为只有两种走法，所以，在保证可以通行的前提下：

f[i][0]=min( f[i-1][0] , f[i][1]+up[i]-down[i] )

f[i][1]=min( f[i-1][1] , f[i][0]+up[i]-down[i] )

注意到f[i][0]与f[i][1]可以互相更新，那可以先令f[i][0]=f[i-1][0],f[i][1]=f[i-1][1]，再用较小的一个去更新另一个即可。具体可以参照std

时间复杂度O(n)，可得100分。